ＡＨＰ（Analytic Hierarchy Process）階層構造に基づく分析法

Ver5.9より、ＡＨＰ分析機能を搭載しました。

Ｔ．Ｌ．サーティ教授（米ピッツバーグ大）によって開発されたもので、集団の意志決定に際し感覚的な部分を計量化し、多数の決定事項を階層化し複数の評価基準をもとに客観的に見いだそうとする手法である。今回、この手法を用いて自施設で採用すべき試薬・機器どれであるのかを決定することを試行してみる。

ＡＨＰ分析の利点は、意思決定の理由を説明する上で根拠のはっきりとしない最終決定のみを提示するのではなく、多数の選択肢の中から重要事項を拾い出し、どのような判断のもとにまとめあげて決定したかを示すことで、より多くの積極的な支持や協力が得られ、決定結果の信頼性を増すことにある。また、複数の人間の共通する感覚に基づくグループ判断を整理することで、個々の考えを理解することも可能となる。ＡＨＰ分析は、方法論が理解しやすく、使いやすいことから多くの問題に適用されている。

現在、ＡＨＰ分析には、サーティ教授が考案した１対比較法から始まり、その後研修者の工夫によって支配型ＡＨＰ、記述的（descrriptive）-ＡＨＰ　（Ｄ－ＡＨＰ）など数多くの手法が考案され、今もなお進化し続けている。

しかし、ＡＨＰ分析も完全なものではなく、意志決定の際の情報不足や適当な代替案や評価項目が選択されていない場合、さらには価値観の相違などによって、異なった判断を下す可能性もあるため、運用には注意を要する。

ＡＨＰ分析の手順は、まず評価項目の整理、モデル階層図の作成、一対比較、総合重要度決定と代替案の比較などを経て解析が行われ決定される。

ＡＨＰの一般的な作業手順について示す。

①.    問題を分析して評価基準項目の抽出と階層図を作成する。

②.    一対比較による評価基準項目のウェイトおよび整合度を算出する。

③.    一対比較による各代替案の評価

④.    代替案の総合評価

※ウェイトの算出や各項目の評価を行う場合には、相対評価法または絶対評価法によって算出する。

では、生化学分析における試薬を選択する場合の具体例を示して説明する。

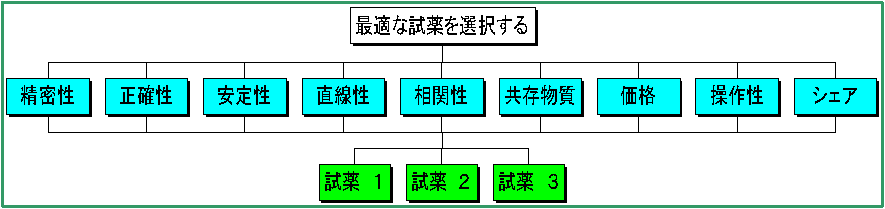
①　階層化：問題を目標、評価基準、代替案に分解し、階層図に書き表す。

まず、目標を階層図の最上層に置き、次に下層に大まかな評価基準、更にその下層に別の評価基準、そして最下層に代替案を並べる。
　例えば階層図の最上層は、今回の目標の「最適な試薬を選択する」とする。次に試薬選択の基準となる評価基準としてＳＴＳＳで検討する「精密性」「正確性」「安定性」「直線性」「相関性」「共存物質の影響」などの基本的性能試験に加え、「価格」や「操作性」「市場シェア」など実際に導入する際に考慮すべき項目を選考基準とする。最後に最下層として比較する試薬名（機器名）を置く。（今回の例では、計算を簡単にするため２レベルの階層を用いているが、精密性や正確性等の基本性能は基本性能として１つにまとめるべきかもしれない。）

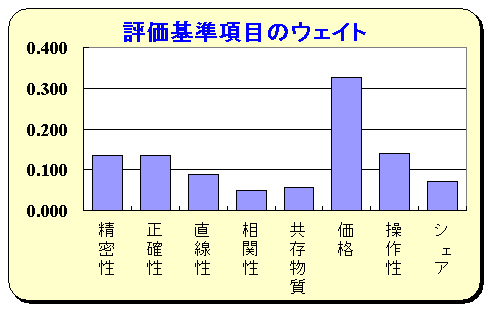
②　評価基準項目のウェイト算出 同一レベルの要素において、各要素の重要度を評価者の主観で判断する。判定するためには、一対比較行列を作成し、重要性の尺度に従って数値を入力する。表へは左側の項目に対する重要性を入力する。右上の青色のセルで数値を選択することで、左下の緑部分は自動計算される。 例えば「精密性」と「安定性」では同程度に重要であると考えれば下表のように[1]を入力する。また、「精密性」と「価格」を比較した場合、「価格」の方が「やや重要」と考えるときは、［１／３］を入力する。一方、対角要素欄は自動計算により［３］が入力される。このような作業をすべての行列について行う。すると各評価基準項目の重要度（ウェイト）およびウェイトグラフが表示される。 なお、試薬を選択する場合の重要性の尺度をどの程度にするかは、各個人の主観によるものであり、数値的に定められたものは今のところない。

重要性の尺度

 

 

※　右上の青枠内に入力すると左下枠内は自動的に計算される。

 

注意：

重要度（ウェイト）算出法には幾何平均法と固有ベクトル法などの方法が提案されている。幾何平均法の方が計算は容易であるが、ここでは固有ベクトル法を用いた重要度算出を行う。これは幾何平均法では整合度：ＣＩ（一対比較の一貫性を表す尺度）を算出することができないため、各重要度判断の間違い等を検出することができないことからである。

CIは，整合度を表す。一般に0.15より大きいとき、一対比較に矛盾があるといわれていることから、見直しまたは一対比較のやり直しを行う。

CI = ( 最大固有値 - n ) / ( n - 1 )　　　　　　　　　n は、行列の列数

 

③　一対比較による各代替案の評価

つづいて、評価基準項目ごとに代替案の一対比較を行う。

例えば、３種類の試薬を検討している場合、「精密性」についてはどのような結果であったかを重要性の尺を基準に入力していく。さらに「安定性」「直線性」・・・について判定してゆく。

 

④　代替案の総合評価

②の評価基準のウェイトと③の代替案のウェイトから、代替案総合評価値を求める。ＳＴＳＳでは、上記２つの重要度を入力すると自動的に総合重要度が算出されグラフ化が行われる。計算式は、各評価基準のウェイト×各代替案のウェイトの合計をもって総合需要度を算出する。なお、ＳＴＳＳでは　画面上見やすくするため、および評価基準ウェイトの変更結果を即座に見るために、　［４．総合評価］を代替案の評価より上に配置している。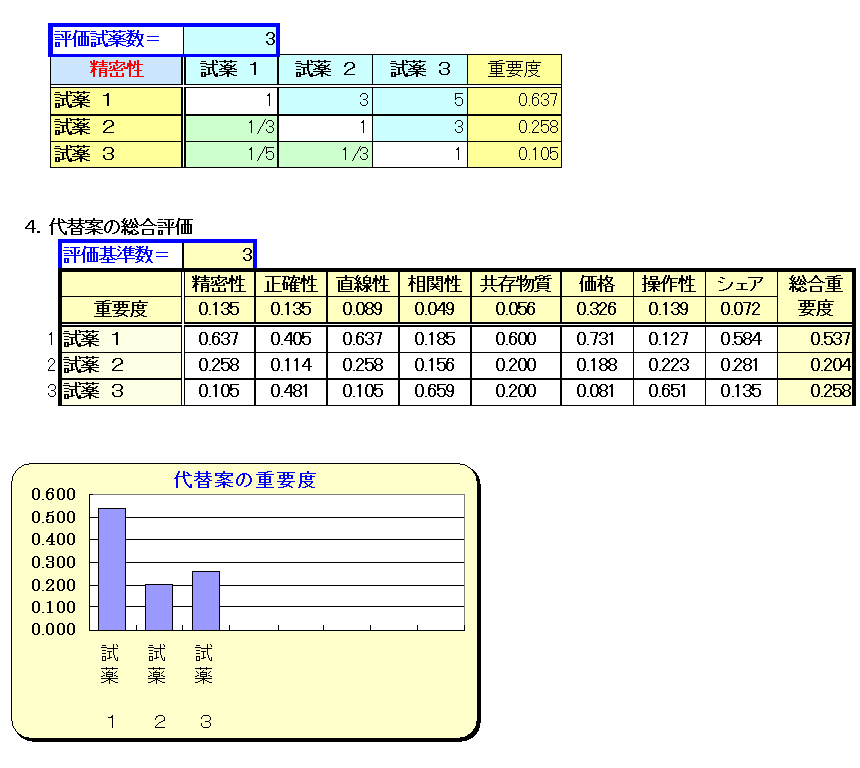

今回示した例は一個人の評価として示したが、複数の人が評価に関わる場合には、各評価者の平均を用いたり、各評価者に対してウェイトをかけるなどの処理によって総合判断することもできる。 しかし、ＡＨＰ分析には、以下のような問題点もある。

a) 代替案が追加された時には一対比較をもう一度やり直す必要がある。 →　多種多様なアイデアは代替案の厚みを増すことになる。

b) 代替案が多くなると整合性が取れなくなる。 →　絶対比較による評価法に変える。

c) 新たな情報によって判断が変化する。→　情報は多い方が信頼性が増す。

d) 一対比較判断が時間とともに変容することもしばしば起こる。 →　考え方の変化もＡＨＰ分析では数値によって判断することができる。 このような場合、総合評価をふまえ再度調査をすることによってより良い結果を生むことになる。なお、Ｅｘｃｅｌによる自動計算により、各評価値の変更が総合評価へどのように影響するのかシミュレーションも容易である。